Linear Interpolation
가장 간단한 보간법
두 점을 이은 직선의 방정식을 근사 함수로 사용한다.
데이터 점들 사이의 간격이 작을수록 더 좋은 근삿값을 얻는다.
$$
\mathrm{g}(x)=\frac{f\left(x_{i+1}\right)-f\left(x_i\right)}{x_{i+1}-x_i}\left(x-x_i\right)+f\left(x_i\right)
$$
Polynomial interpolation
(n+1)개의 점이 주어진 경우 n차 이하의 유일한 다항식을 구할 수 있다.
-
Q. n+1개의 점으로 찾을 수 있는 n차 다항식은 왜 유일한가?
방데르몽드 행렬
각 행의 초항이 1인 등비수열로 이루어진 행렬
$$ V=\left(\begin{array}{ccccc}1 & \alpha_1 & \alpha_1^2 & \cdots & \alpha_1^{n-1} \\ 1 & \alpha_2 & \alpha_2^2 & \cdots & \alpha_2^{n-1} \\ 1 & \alpha_3 & \alpha_3^2 & \cdots & \alpha_3^{n-1} \\ \vdots & \vdots & \vdots & & \vdots \\ 1 & \alpha_m & \alpha_m^2 & \cdots & \alpha_m^{n-1}\end{array}\right) $$방데르몽드 행렬
$V$에 대해 다음과 같이 일반화할 수 있다.$$ \operatorname{det} V=\prod_{i<j}\left(\alpha_i-\alpha_j\right) $$따라서,
$a_0,a_1,...,a_n$이 서로 다른 값을 가진다면$V$는 역행렬이 존재한다.가역 행렬의 기본 정리에 의해
$\tt Vx = b$의 해는 유일하다.
이제 다항식을 찾아내는 세 가지 방법을 알아보자.
미정 계수법
다항식을 찾는 가장 보편적인 방법
보간 다항식 $p(x) = a_0 + a_1x + a_2x^2 + ... + a_nx^n$에 대해
-
주어진
$n+1$개의 점을$p(x)$에 대입하여 연립 방정식을 생성한다.모두 다 대입하면 아래와 같이 방데르몽드 행렬식 형태를 얻을 수 있다.
$$ \begin{array}{cc}p\left(x_0\right)=f\left(x_0\right) & a_0+a_1 x_0+a_2 x_0^2+\cdots+a_n x_0^n=f\left(x_0\right)\\ p\left(x_1\right)=f\left(x_1\right) & a_0+a_1 x_1+a_2 x_1^2+\cdots+a_n x_1^n=f\left(x_1\right)\\ \vdots & \vdots \\ p\left(x_n\right)=f\left(x_n\right) & a_0+a_1 x_n+a_2 x_n^2+\cdots+a_n x_n^n+\left(x_n\right)\end{array} $$$$ \left[\begin{array}{ccccc}1 & x_0 & x_0^2 & \cdots & x_0^n \\ 1 & x 1 & x_1^2 & \cdots & x_1^n \\ & & & \cdots & \\ 1 & x_n & x_n^2 & \cdots & x_n^n\end{array}\right]\left[\begin{array}{l}a 0 \\ a 1 \\ \cdots \\ a n\end{array}\right]=\left[\begin{array}{c}f\left(x_0\right) \\ f\left(x_1\right) \\ \cdots \\ f\left(x_n\right)\end{array}\right] $$ -
가우스 소거법 등으로 연립 방정식의 해를 구한다.
단점
- 느린 계산 시간
- 오차 발생
Lagrange Interpolation(라그랑주 보간법)
연립 방정식을 풀지 않고 다항식을 결정하는 방법
특정 숫자를 대입하면 0이나 1이 되는 항을 만든다.
$(x-a)$를 곱해주면$x$에 a값을 대입할 때 0이 된다.$(x-a)$를$(b-a)$로 나누면,$x$에$b$를 대입했을 때 1이 된다.
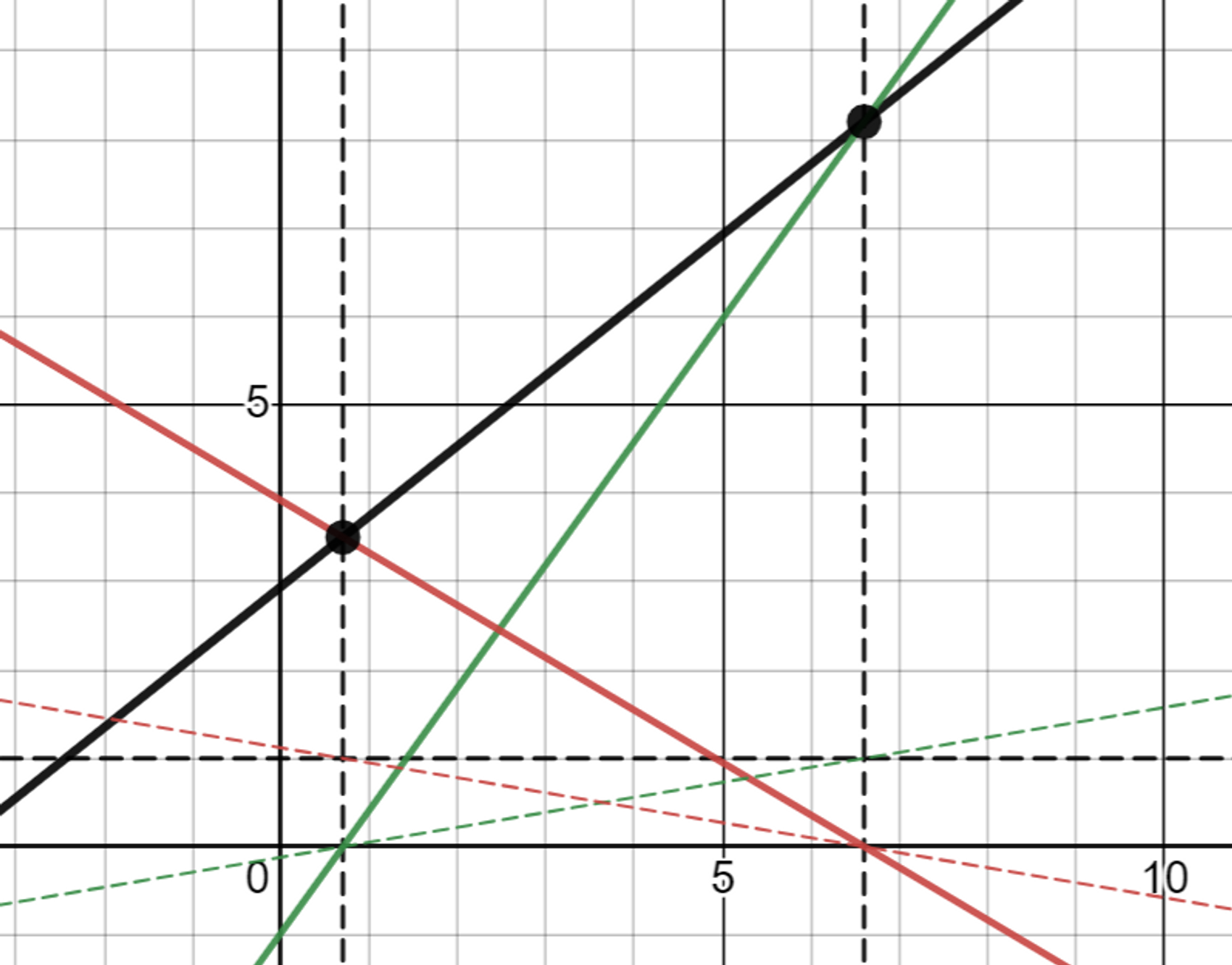
1차 함수
두 점$(x_0, y_0), (x_1, y_1)$이 주어진 경우
$$
y=\left(\frac{x-x_1}{x_0-x_1}\right) y_0+\left(\frac{x-x_0}{x_1-x_0}\right) y_1
$$
위 식에 $x_0$을 대입하면 $y_0$이 나오고, $x_1$을 대입하면 $y_1$이 나온다.
해당 식은 직관적으로 $(x_0,0),(x_1,y_1)$을 지나는 직선의 기울기와 $(x_0,y_0),(x_1,0)$을 지나는 직선의 기울기의 합으로 이해할 수 있다.
2차 함수
세 점$(x_0, y_0), (x_1, y_1), (x_2, y_2)$이 주어진 경우
$$
y=\left(\frac{\left(x-x_1\right)\left(x-x_2\right)}{\left(x_0-x_1\right)\left(x_0-x_2\right)}\right) y_0+\left(\frac{\left(x-x_2\right)\left(x-x_0\right)}{\left(x_1-x_2\right)\left(x_1-x_0\right)}\right) y_1\\
+\left(\frac{\left(x-x_0\right)\left(x-x_1\right)}{\left(x_2-x_0\right)\left(x_2-x_1\right)}\right) y_2
$$
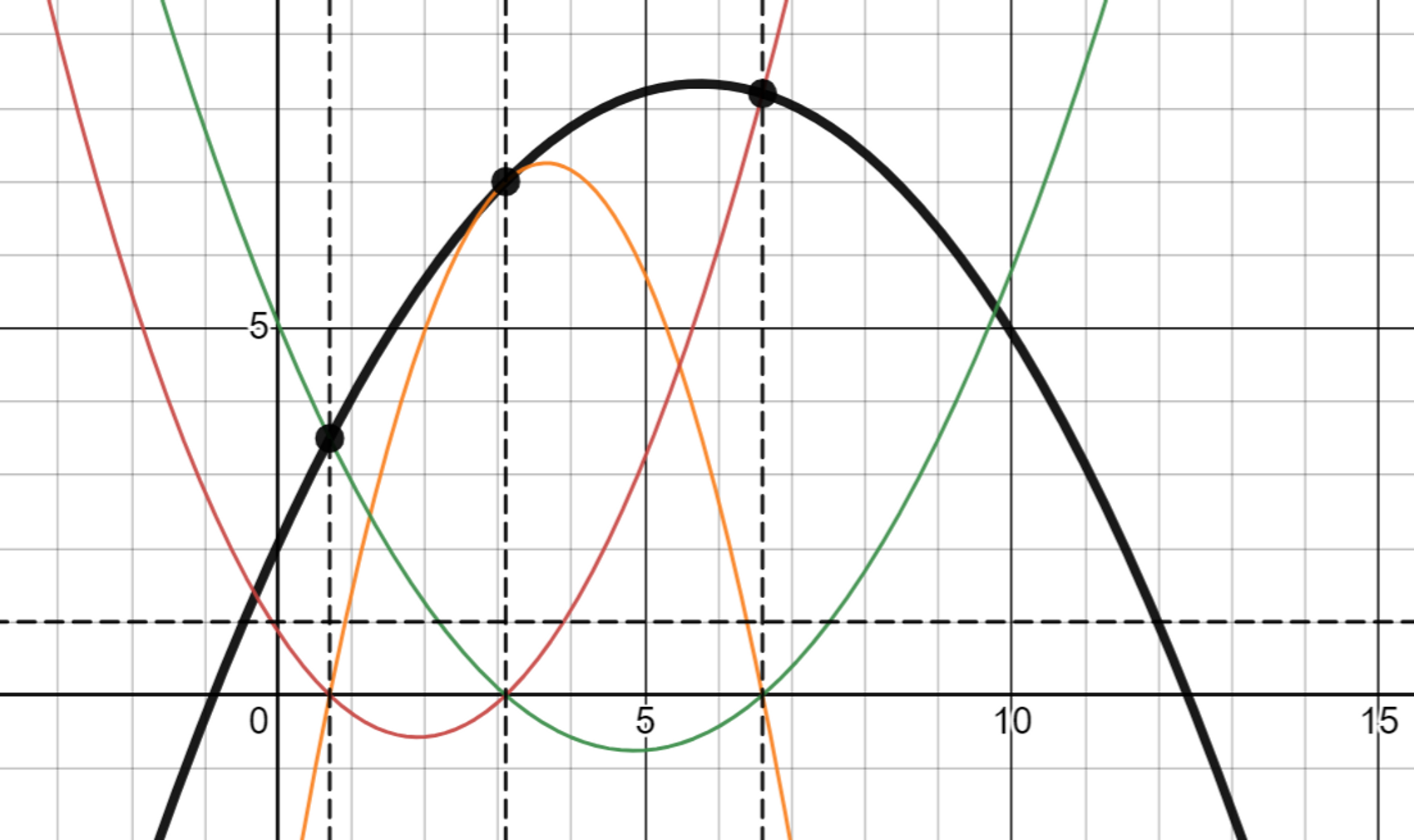
마찬가지로, $(x_i,y_i)$를 지나면서 $(x_j,0)$을 지나는 이차 함수의 기울기의 합으로 이해할 수 있다.
3차 함수
네 점이 주어진 경우
$$
y=\left(\frac{\left(x-x_1\right)\left(x-x_2\right)\left(x-x_3\right)}{\left(x_0-x_1\right)\left(x_0-x_2\right)\left(x_0-x_3\right)}\right) y_0\\
+\left(\frac{\left(x-x_2\right)\left(x-x_3\right)\left(x-x_0\right)}{\left(x_1-x_2\right)\left(x_1-x_3\right)\left(x_1-x_0\right)}\right) y_1\\
+\left(\frac{\left(x-x_0\right)\left(x-x_1\right)\left(x-x_3\right)}{\left(x_2-x_0\right)\left(x_2-x_1\right)\left(x_2-x_3\right)}\right) y_2\\
+\left(\frac{\left(x-x_0\right)\left(x-x_1\right)\left(x-x_2\right)}{\left(x_3-x_0\right)\left(x_3-x_1\right)\left(x_3-x_2\right)}\right) y_3
$$
일반화
$$
L_i(x)=\prod_{\substack{j=0 \\ j \neq i}}^n \frac{x-x_j}{x_i-x_j}
$$
위의 식은 곧 $x_i$를 넣었을 때 $y_i$가 나온다는 것을 의미한다.
$$
\begin{matrix}P_n(x)&=&L_0(x) f\left(x_0\right)+L_1(x) f\left(x_1\right)+\cdots L_n(x) f\left(x_n\right)\\
&=&\sum_{i=0}^n L_{i(x)} f\left(x_i\right)
\end{matrix}
$$
Q. 단일 함수를 구할 수 있는가?
$P_n\left(x_i\right)=y_i$를 만족하므로 $\mathrm{n}+1$개의 점 $\left(x_i, y_i\right)$을 지나는 유일한 $\mathrm{n}$차 다항식이다.
Q. 연산량이 기존 방법과 비교했을 때 늘어나는가, 줄어드는가?
단점
-
차수가 커지면 참 값을 기대할 수 없을 정도의 오차가 발생한다.
-
데이터의 수가 증가할 때, 바로 직전의 결과를 사용하지 못한다.
점이 추가되면 식을 처음부터 다시 계산해야 한다.
-
하나의 보간을 위해 필요한 계산량이 많다.
그렇다면, 식을 처음부터 다시 계산하지 않는 방법은 없을까?
결국 라그랑주 보간법은 각 점을 지나는 함수의 기울기를 합산하는 방식이기 때문에, 기울기가 중복으로 계산되는 지점을 제거하여 연산량을 줄일 수 있다. 이를 위해 Divided Difference이 쓰인다.
Newton’s divided differences interpolation
라그랑주 보간법의 모든 단점을 해결하는 방법
- 점 두 개로 일차 함수를 먼저 그린 후, 점을 추가해나가며 다항식의 차수를 점점 확장해나가는 방식
- 연립 일차 방정식을 사용하지 않는다.
- 뉴턴 형을 활용한다.
Divided Differences(분할 차분법)
간단 요약
분할 구간에서 함수값들의 차이
기울기에 대한 이산적인 추정치로 사용할 수 있다.
뉴턴 형이 주어졌을 때, 상수 항들을 어떻게 계산해야 할까?
뉴턴 형
서로 다른 점 $x_0, ..., x_n$에 대해 x값에 따라 상수 항들을 순서대로 구할 수 있는 형태
$$
\begin{matrix}P_n(x)=a_0+a_1\left(x-x_0\right)
+a_2\left(x-x_0\right)\left(x-x_1\right)+\\
\ldots+a_n\left(x-x_0\right)\left(x-x_1\right) \ldots\left(x-x_{n-1}\right)\end{matrix}
$$
식이 복잡하게 생겼다. $P_n(x) = f(x)$라 정의하고, 식을 상수 항 기준으로 정리해보자.
$a_0, a_1$ 도출 과정
$$
a_0 = f\left(x_0\right)\\
f(x_1) = a_0 + a_1(x_1-x_0),\\
\therefore a_1 = {f\left(x_1\right) - f(x_0)\over x_1-x_0}
$$
해당 식의 형태를 $f[x_0,x_1]$로 치환하자.
이는 first order Divided Difference라고 부른다.
first order Divided Difference
$$
f\left[x_0, x_1\right]=\frac{f\left(x_1\right)-f\left(x_0\right)}{x_1-x_0}
$$
한글로 번역하면 1차 분할 차분인데, 이는 위의 수식이 1차 미분에 대한 이산적인 추정치로 쓰일 수 있기 때문이다.
만약 $f(x)$가 구간 $[x_0,x_1]$에서 미분 가능하다면, 평균값 정리에 의해$f\left[x_0, x_1\right]=f^{\prime}(c)$임을 보장한다.
$a_2$ 도출 과정
$$
\begin{matrix}
f(x_2) &=& a_0 + a_1(x_2 - x_0) + a_2(x_2-x_0)(x_2-x_1)\\
&=& f(x_0) + (x_2 - x_0)(a_1 + a_2(x_2 - x_1)),\\
f(x_2) - f(x_0) &=& (x_2-x_0)(a_1 + a_2(x_2 - x_1))
\end{matrix}
$$
이고, 이를 좀 더 정리하면
$$
\frac{f(x_2)-f(x_0)}{x_2-x_0} = a_1 + a_2(x_2 - x_1)
$$
이 된다.
여기서, $a_1$과 $a_2$에서 반복되는 형태를 $f[x_a,x_b]$로 치환하자.
$$
f[x_0,x_2] = f[x_0,x_1] + a_2(x_2 - x_1)\\
\frac{f[x_0,x_2] - f[x_0,x_1]}{x_2 - x_1} = a_2\\
$$
위 식은 $f[x_0,x_1,x_2]$로 치환하며, Second order Divided Difference라고 부른다.
High order Divided Difference
$$
f\left[x_0, x_1, x_2\right]=\frac{f\left[x_1, x_2\right]-f\left[x_0, x_1\right]}{x_2-x_0}
$$
$$
f\left[x_0, x_1, x_2, x_3\right]=\frac{f\left[x_1, x_2, x_3\right]-f\left[x_0, x_1, x_2\right]}{x_3-x_0}
$$
$$
f\left[x_0, \ldots, x_n\right]=\frac{f\left[x_1, \ldots, x_n\right]-f\left[x_0, \ldots, x_{n-1}\right]}{x_n-x_0}
$$
이와 같은 형태로 나머지 $a_n$에 대해서도 정리할 수 있고, 최종적으로 기존의 뉴턴 형은 다음과 같은 형태가 된다.
$$
\begin{aligned}& P_1(x)=f\left(x_0\right)+\left(x-x_0\right) f\left[x_0, x_1\right] \\
& \begin{aligned}P_2(x)=f\left(x_0\right) & +\left(x-x_0\right) f\left[x_0, x_1\right] \\
& +\left(x-x_0\right)\left(x-x_1\right) f\left[x_0, x_1, x_2\right]\end{aligned}\\
&\ \ \ \ \ \ \ \ \ \ \ \ \vdots\\
&\begin{aligned}P_n(x)=f\left(x_0\right) & +\left(x-x_0\right) f\left[x_0, x_1\right]+\cdots \\
& +\left(x-x_0\right)\left(x-x_1\right) \cdots\left(x-x_{n-1}\right) f\left[x_0, x_1, \ldots, x_n\right]\end{aligned}\end{aligned}
$$
여기에서 중요한 점은, 기호화를 함으로써 값을 재활용할 수 있게 되었다는 것이다.
또한, 기존의 값을 활용하여 다음 값을 구할 수 있게 되었다.
최종적으로 뉴턴 공식을 일반화하여 정리하면 다음과 같은 형태가 된다.
$$
\begin{aligned}P_n(x) & =f\left[x_0\right]+f\left[x_0, x_1\right]\left(x-x_0\right)+\cdots\\
&\ \ \ \ \ \ \ \ \ \ \ \ \ \ +f\left[x_0, \cdots, x_n\right]\left(x-x_0\right) \cdots\left(x-x_{n-1}\right) \\
& =f\left[x_0\right]+\sum_{k=1}^n f\left[x_0, \cdots, x_k\right]\left(x-x_0\right) \cdots\left(x-x_{k-1}\right) \\
& =f\left[x_0\right]+\sum_{k=1}^n f\left[x_0, \cdots, x_k\right] \prod_{i=0}^{k-1}\left(x-x_i\right)\end{aligned}
$$
이를 점화식의 형태로 정리하면 다음과 같다.
$$
p_{n+1}(x)=p_n(x)+f[x_0, x_1, \cdots, x_n, x_{{n+1}}] \prod_{j=0}^n(x-x_j)
$$
2. Error in polynomial interpolation
보간 다항식은 결국 실제 함수에 대한 추정이기 때문에, 오차가 존재한다.
라그랑주 보간법의 오차를 계산해보자.
앞에서 $P_n(x)$를 다음과 같이 정리했다.
$$
\begin{matrix}P_n(x)&=&L_0(x) f\left(x_0\right)+L_1(x) f\left(x_1\right)+\cdots L_n(x) f\left(x_n\right)\\
&=&\sum_{i=0}^n L_{i(x)} f\left(x_i\right)
\end{matrix}
$$
$f(x):$구간$[a,b]$에서 정의된 함수(실제 함수)$p_n(x): n+1$$n+1$$f(x)$의 보간 다항식
이라 했을 때, 다음이 성립한다.
$$
f(x)=P_n(x) + \frac{\left(x-x_0\right)\left(x-x_1\right) \cdots\left(x-x_n\right)}{(n+1) !} f^{(n+1)}\left(c_x\right)
$$
-
$c_x : [a,b]$구간 내 임의의 점 -
증명 과정
-
실제 함수
$f(x)$와 보간 다항식$P_n(x)$의 차이에 대한 함수를$R_n(x)$라 하자.$(x \neq x_k)$즉,
$f(x) = P_n(x) + R_n(x)$가 성립하는 상황에서,$R_n(x)$는$x_k$마다 0이 되기 때문에 다음과 같이 정의할 수 있다.$$ R_n(x)=C \prod_{k=0}^n\left(x-x_k\right) $$$C$는 상수를 의미한다.
-
새로운 함수
$F(x)$를$$ F(x) = f(x) - P_n(x) - R_n(x) $$라고 할 때,
-
**롤의 정리(Rolle’s Theorem)**에 의해
$\mathrm{n}$개 점에서 함수가 0이면,$\mathrm{n}-1$차 미분의 값이 0인 점이 존재한다.$\mathrm{g}(\mathrm{t})$는$x, x_0, x_1, \ldots, x_n$의 구간으로$\mathrm{n}+2$개의 함수가 0 인 점이 존재하므로,$\mathrm{n}+1$차 미분이 0 인 점$c_x$가 존재한다.$$ f^{n+1}(c_x)-P^{n+1}(c_x)-[f(x)-P(x)] \frac{d^{n+1}}{d t^{n+1}}\left[\Pi_{i=0}^n \frac{t-x_i}{x-x_i}\right]_{t=c_x} $$$\mathrm{P}$는 최대$\mathrm{n}$차식이므로$P^{n+1}=0$
-
$g^{n+1}(c_x)=0=f^{n+1}(c_x)-0-f(x)-P(x) ! \Pi_{i=0}^n \frac{1}{x-x_i}$$\left(t-x_i\right)$는$\mathrm{n}+1$차항이므로$\mathrm{n}+1$번 미분하면$(\mathrm{n}+1)!$
-
위 식을
$\mathrm{f}(\mathrm{x})$에 대해 정리하면 다음과 같다.$$ f(x)=P(x)+\frac{f^{n+1}(c_x)}{(n+1) !}\left(x-x_0\right)\left(x-x_1\right) \ldots\left(x-x_n\right) $$
결론적으로, 오차(실제 함수 - 보간 다항식)는 다음과 같이 정의된다.
$$ e_n(x)=f(x)-P_n(x) $$$$ f(x)-P(x)=\frac{f^{n+1}(c_x)}{(n+1) !}\left(x-x_0\right)\left(x-x_1\right) \ldots\left(x-x_n\right) $$- 최대 오차는
$\max \|\frac{f^{n+1}(c_x)}{(n+1) !}\| \cdot \max \|\left(x-x_0\right)\left(x-x_1\right) \ldots\left(x-x_n\right)\|$
-
-
$f(x):$구간$[a,b]$에서 정의된 함수(실제 함수) -
$p_n(x): n+1$$n+1$$f(x)$의 보간 다항식이라 했을 때, 오차(실제 함수 - 보간 다항식)는 다음과 같이 정의된다.
$$
e_n(x)=f(x)-p_n(x)
$$
따라서 다음이 성립한다.
$$
\begin{aligned}
& p_{n+1}\left(x_i\right)=f\left(x_i\right), \quad i=0,1,2, \cdots, n \\
& p_{n+1}(\bar{x})=f(\bar{x})
\end{aligned}
$$
뉴턴 공식으로 다시 표현하면
$$
p_{n+1}(x)=p_n(x)+f\left[x_0, x_1, \cdots, x_n, \bar{x}\right] \prod_{j=0}^n(x-x_j)
$$
과 같고, 이 때의 $f(x)$는 다음과 같다.
$$
f(\bar{x})=p_{n+1}+f\left[x_0, x_1, \cdots, x_n, \bar{x}\right) \prod_{j=0}^n\left(\bar{x}-x_j\right)
$$
아래에서 표현된 식들로 오차에 대한 식을 다시 정리해보면
$$
e_n(\bar{x})=f\left[x_0, x_1, \cdots, x_n, \bar{x}\right] \prod_{j=0}^n\left(\bar{x}-x_j\right)
$$
위처럼 나타낼 수 있다.
그렇다면 과연 뉴턴 보간법은 단점이 없을까? 그렇지 않다.
3. Spline Interpolation
뉴턴 보간법과 라그랑주 보간법은 계단 함수와 같은 급격한 불연속을 잘 표현하지 못한다.
-
Runge 현상
Runge 함수는 Polynomial로 적합이 잘 되지 않는 함수로 알려져 있다.
$$ f(x)=\frac{1}{1+25 x^2} $$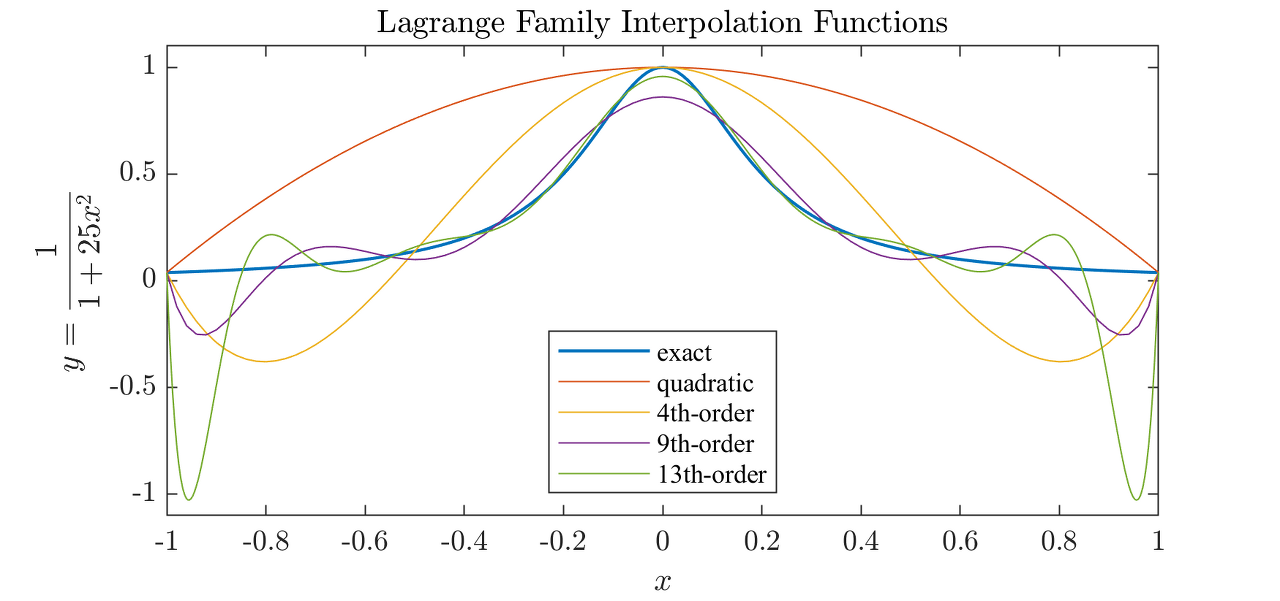
-
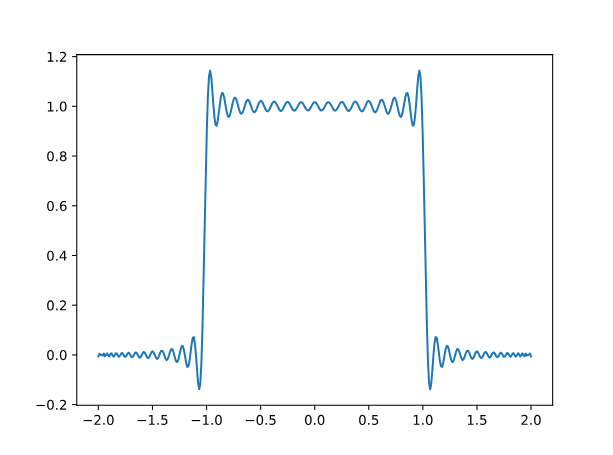
Gibbs 현상 불연속 함수를 근사할 때 불연속 값 근처에서 나타나는 불일치 현상
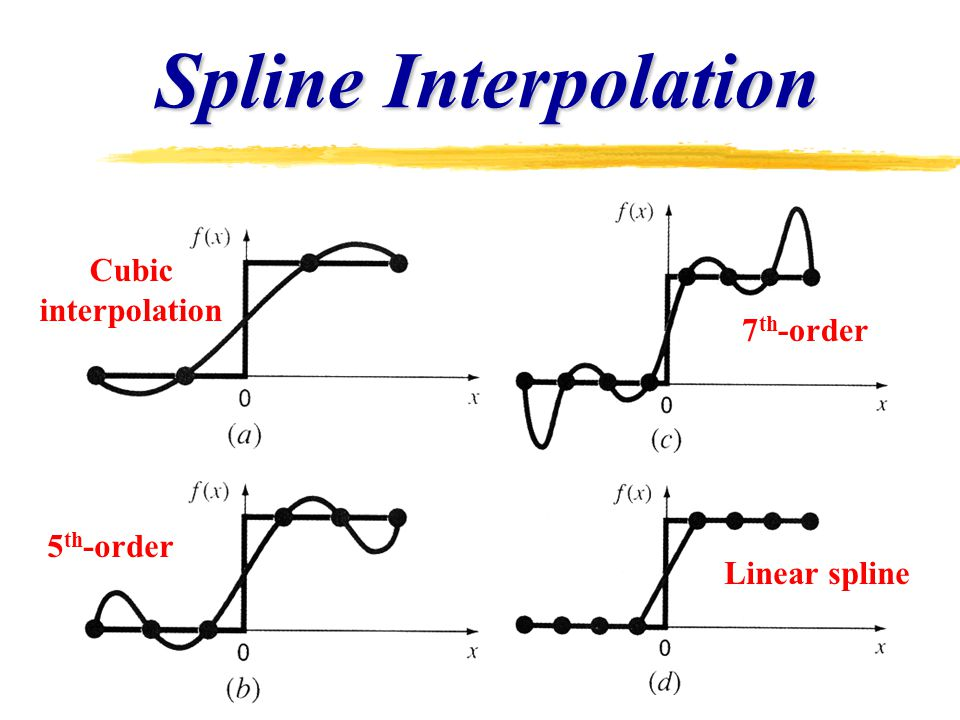
Piecewise Polynomials Interpolation
여러 개의 데이터를 하나의 추정 함수로 표현하지 않고, 구간 별로 추정 함수를 구하는 것
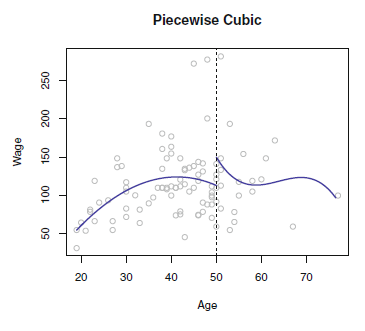사진은 Interpolation이 아니라 Regression에 해당하지만, Piecewise Polynomial에 대한 이해를 돕기 위해 가져왔다.
다만, 사진처럼 knot에서 불연속이기 때문에, 합리적이지 않은 추정 함수가 나올 수 있다.
Continuous Piecewise Polynomials Interpolation
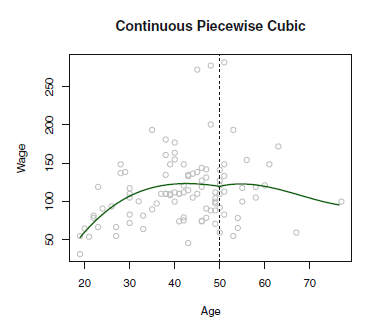
Piecewise에 연속이라는 제약 조건을 추가했다.
하지만 여전히 만족스럽지 않다.
Spline
- 각 지점(knots)에서 자기 자신과 1차 미분 함수부터
$d-1$차 미분 함수까지 모두 연속이다. - knot에서 함수의 계수가 변하므로 knot가 많을 수록 더 유연하게 된다.
점과 점 사이를 그저 연결하면 Linear Spline이 되기 때문에, 선형 스플라인은 잘 활용하지 않는다.
2차 Spline부터 알아보자.
Quadratic Spline Interpolation
n+1개의 점을 연결하는 n개의 2차 다항식을 추정하고자 한다.
각 2차 다항식마다 $ax^2 + bx + c$와 같이 3개의 미지수가 존재하기 때문에,
모든 다항식을 추정하기 위해서 $3n$개의 조건이 필요하다.
이러한 $3n$개의 조건은 적절한 제약을 추가하여 얻을 수 있다.
-
첫 번째 함수와 맨 마지막 함수는 각각 첫 번째 점과 마지막 점을 지나야 한다.
이로부터 2개의 조건을 얻을 수 있다.
$
\begin{aligned}& f\left(x_0\right)=a_1 x_0^2+b_1 x_0+c_1 \\ & f\left(x_n\right)=a_n x_n^2+b_n x_n+c_n\end{aligned}$이제 나머지 n개의 조건을 얻으면 된다.
-
양 끝을 제외한 n-1개의 점에서 함수가 연속해야 한다.
즉, 각 내부의 점에서 n개의 함수는 양 끝 점을 지나야 한다.
이로부터
$2n-2$개의 조건을 얻을 수 있다.$i=2\dots n$일 때,$f\left(x_{i-1}\right)=a_{i-1} x_{i-1}^2+b_{i-1} x_{i-1}+c_{i-1}:$주어진$i-1$번째 데이터의 왼쪽 함수$f\left(x_{i-1}\right)=a_i x_{i-1}^2+b_i x_{i-1}+c_i:$주어진$i-1$번째 데이터의 오른쪽 함수 -
모든 점에서 함수가 매끄러워야 한다. 즉, 모든 knots에서 미분 가능해야 한다.
$i=2\dots n$일 때,$f^{\prime}\left(x_{i-1}\right)=2 a_{i-1} x_{i-1}+b_{i-1}$: 주어진$i-1$번째 데이터의 왼쪽 1차 도함수$f^{\prime}\left(x_{i-1}\right)=2 a_i x_{i-1}+b_i$: 주어진$i-1$번째 데이터의 왼쪽 1차 도함수이를 통해
$n-1$개의 조건을 얻을 수 있다.이제 단 하나의 조건만 있으면 된다.
-
첫 번째 함수의 이계 도함수는 0이다. 즉, 첫 번째 함수는 직선이다.
$f_1''(x_0) = a_1 = 0$
이렇게 총 $3n$개의 조건을 얻었으므로, $n$개의 2차 다항식을 추정할 수 있다.
Cubic Spline Interpolation
2차 Spline 보간법과 마찬가지 이유로 이번에는 $4n$개의 조건이 필요하다.
- 첫 번째와 마지막 함수는 각 양 끝 점을 지난다. →
$2$ - 연속 →
$2n - 2$ - 미분 가능(1계 도함수 연속) →
$n-1$ - 2계 도함수 연속 →
$n-1$
여기까지 계산하면 총 $4n - 2$로 2개의 조건이 부족해 유일 해를 구할 수 없다.
따라서 다음과 같은 임의의 조건을 추가하여 유일 해를 채울 수 있다.
- 첫 번째 함수와 마지막 함수의 2계 도함수는 0이어야 한다. →
$2$
이러한 다섯 개의 조건으로 보간된 곡선을 Natural Cubic Spline이라고 한다.
4차 이상의 고차 스플라인은 내재된 불안정성 때문에 잘 사용하지 않기 때문에, Cubic Spline을 가장 많이 활용한다.
참고 자료
회귀 스플라인 (Regression Spline)에 대한 이해
[interpolation] - Spline method
[ISL] 7장 -비선형모델(Local regression, Smoothing splines, GAM) 이해하기 · Go’s BLOG