간단 요약
행렬을 인수분해 후 재생성하여 결측치를 예측하는 방법
인수분해를 다양하게 시도하여 대상 행렬을 가장 잘 복구하는 최적의 하위행렬을 찾는 과정
Latent Factors, Matrix Factorization, SGD
행렬을 인수분해 후 재생성하여 결측치를 예측하는 방법
-
대상 행렬을 두개의 하위 행렬로 분해한다.
User-Item 행렬을 User와 Item 각각에 대한 저차원의 latent factor 행렬로 분해한다.
-
두 하위 행렬을 다시 곱해서 대상 행렬과 동일한 크기의 단일 행렬로 만든다.
-
위의 과정에서 기존 행렬의 빈공간이 채워진다.
이는 행렬의 성질을 이용한 것이다.
즉, 결측값(비평가 항목)에 대해 임의로 Imputation을 수행하지 않는다.
실제로 관측된 값만 활용한다.
요약하면, 인수분해를 다양하게 시도하여 대상 행렬을 가장 잘 복구하는 최적의 하위행렬을 찾는 과정이다.
기계가 해석하기 위한 행렬, 즉 블랙 박스 모델에 더 가깝다.
추천시스템에서 두 개의 하위행렬은 각각 유저 임베딩(User Latent Factors)과 아이템 임베딩(Item Latent Factors)이 된다.
결국 MF를 학습하는 것은 latent feature들을 학습하는 것과 같다.
범주형 feature의 잠재 요인을 feature로 사용하고자 할 경우 이 잠재 요인을 가장 손쉽게 구할 수 있는 방법이다.
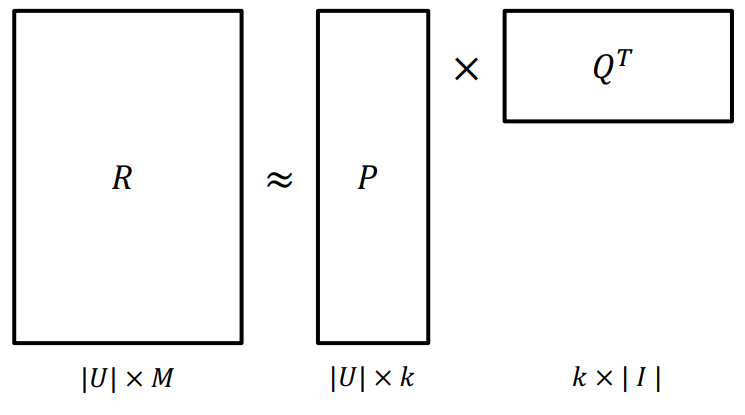
Latent 행렬을 각각 P, Q라고 했을 때, MF는 Rating Matrix를 $P$와 $Q$로 분해하여 $R$과 최대한 유사하게 $\hat R$을 추론한다.(최적화)
$$
R \approx P \times Q^T = \widehat R
$$
모델 학습 과정
Object Function을 정의하고 최적화 문제를 푸는 모델학습 과정을 살펴보자.
$$
R \approx P \times Q^T = \widehat R\\
P \rightarrow |U| \times k\\
Q \rightarrow |I| \times k
$$
Objective Function
기본 형태
$$
\tt \min _{P, Q} \sum_{\text {observed } r_{u, i}}\left(r_{u, i}-p_u^T q_i\right)^2
$$
-
$r_{u,i}:$학습 데이터에 있는 유저$u$의 아이템$i$에 대한 실제 rating -
$p_u,q_i:$유저($u$)와 아이템($i$)의 latent vector학습을 통해 알아내고자 하는 목표
최적화 문제를 통해 갱신되는 파라미터
-
$\widehat {r_{u,i}} = p_u^Tq_i$: 예측된 Rating Matrix-
원본 수식처럼
$p \times q^T$가 아닌$p^T \times q$인 이유우선,
$r_{u,i}$,$p_{u,x}$, 그리고$q_{x,i}$는 각각 다음을 의미한다.($Q^T$헷갈리지 않게 주의)$r_{u,i}$:$R$의$(u,i)$번째 원소$p_{u,x}$:$P$의$(u,x)$번째 원소$q_{x,i}$:$Q^T$의$(x,i)$번째 원소또한, 행렬 연산에서 벡터는 보통 “열벡터(column vector)“를 의미하므로
$P$의$u$번째 행($p_{u,1:k}$)은$P^T$의$u$번째 열($p^T_{1:k,u}$), 즉$p^T_u$로 표현할 수 있다.따라서, 해당 공식에서
$R$의$(u,i)$번째 원소의 추정치인$\widehat{r_{u,i}}$는$P^T$의$u$번째 열벡터($p^T_u$)와$Q^T$의$i$번째 열벡터($q_i$)를 곱한 값이라고 할 수 있다.물론,
$\widehat{r_{u,i}}$는$1 \times 1$크기의 행렬이므로 우측 항에 전치를 취해도 결과가 동일하다.(
$\therefore \widehat{r_{u,i}} = p^T_u \cdot q_i = q^T_i \cdot p_u$)
-
최종 형태
$$
\tt \min _{P, Q} \sum_{\text {observed }r_{u,i}}\left(r_{u, i}-p_u^T q_i\right)^2
+{\lambda\left(\left\|p_u\right\|_2^2+\left\|q_i\right\|_2^2\right)}
$$
$\lambda$(상수)배 된 penalty term은 L2 — Regularization(규제)
학습 데이터에 과적합되는 것을 방지한다.
MF 학습
SGD: Stochastic gradient descent(확률적 경사 하강법)
MF 모델에서의 SGD
-
Error
$e_{ui}$`$$ \tt e_{u i}=r_{u i}-p_u^T q_i
$$`
-
Loss
$L$$$ \tt L=\sum\left(r_{u, i}-p_u^T q_i\right)^2+\lambda\left(\left\|p_u\right\|_2^2+\left\|q_i\right\|_2^2\right) \quad $$Loss를
$p_u$로 미분하여 최솟값 계산 -
Gradient
$$ {\tt{\frac{\partial L}{\partial p_u}=\frac{\partial\left(r_{u i}-p_u^T q_i\right)^2}{\partial p_u}+\frac{\partial \lambda\left\|p_u\right\|_2^2}{\partial p_u}}}\\\tt{ \\=-2\left(r_{u i}-p_u^T q_i\right) q_i+2 \lambda p_u} $$이를 Error Term을 활용하여 아래와 같이 나타낼 수 있다.
$$ \tt \frac{\partial L}{\partial p_u}=-2\left(e_{u i} q_i-\lambda p_u\right) $$ -
Gradient의 반대 방향으로
$p_u$,$q_i$를 업데이트$$ {\tt \\p_u \leftarrow p_u+\eta \cdot\left(e_{u i} q_i-\lambda p_u\right)}\\ \tt q_i \leftarrow q_i+\eta \cdot\left(e_{u i} p_u-\lambda q_i\right) $$부호가 바뀐다.
MF 기반 추천으로 가장 널리 알려진 논문
Matrix Factorization Techniques for Recommender Systems
기본적인 MF에 다양한 테크닉을 추가하여 성능을 향상시켰다.
-
Adding Biases
어떤 유저는 모든 영화에 대해 평점을 낮게 줄 수도 있다.
아이템도 마찬가지로 편향이 발생할 수 있다.
⇒ 전체 평균
$\mu$, 유저, 아이템의 bias를 추가하여 예측 성능을 높인다.-
기존 목적 함수
$$ \tt \min _{P, Q} \sum_{\text {observed }r_{u,i}}\left(r_{u, i}-p_u^T q_i\right)^2+\lambda\left(\left\|p_u\right\|_2^2+\left\|q_i\right\|_2^2\right) $$ -
Bias가 추가된 목적 함수
$$ {\tt \min _{P, Q} \sum_{\text {observed } r_{u,i}}\left(r_{u, i}-{\mu - b_u-b_i}-p_u^T q_i\right)^2} \\+\tt \lambda\left(|| p_u\left\|_2^2+|| q_i\right\|_2^2+{b_u^2+b_i^2}\right) $$마찬가지로 bias가 규제 term에 추가되어 과적합되지 않게 한다.
-
Error
$$ \tt e_{u,i} = r_{u,i} - \mu - b_u - b_i - p_u^Tq_i $$ -
Gradient의 반대방향으로
$\tt b_u, b_i, x_u, y_i$를 업데이트$$ \begin{aligned}& {b_u \leftarrow b_u+\gamma \cdot\left(e_{u i}-\lambda b_u\right)} \\& {b_i \leftarrow b_i+\gamma \cdot\left(e_{u i}-\lambda b_i\right) } \\& p_u \leftarrow p_u+\gamma \cdot\left(e_{u i} q_i-\lambda p_u\right) \\& q_i \leftarrow q_i+\gamma \cdot\left(e_{u i} p_u-\lambda q_i\right)\end{aligned} $$
-
-
Adding Confidence Level
모든 평점이 동일한 신뢰도를 갖지 않는다. ⇒
$r_{u,i}$에 대한 신뢰도를 의미하는$c_{u,i}$를 추가-
대규모 광고 집행과 같이 특정 아이템이 많이 노출되어 클릭되는 경우
-
유저의 아이템에 대한 평점이 정확하지 않은 경우(implicit Feedback)
-
기존 목적 함수
$$ {\tt \min _{P, Q} \sum_{\text {observed } r_{u,i}}\left(r_{u, i}-\mu-b_u-b_i-p_u^T q_i\right)^2} \\+\tt\lambda\left(|| p_u\left\|_2^2+|| q_i\right\|_2^2+b_u^2+b_i^2\right) $$ -
Confidence Level이 추가된 목적함수
$$ {\tt \min _{P, Q} \sum_{\text {observed } r_{u, i}} {c_{u, i}}\left(r_{u, i}-\mu-b_u-b_i-p_u^T q_i\right)^2}\\+\tt\lambda\left(|| p_u\left\|_2^2+|| q_i\right\|_2^2+b_u^2+b_i^2\right) $$
-
-
Adding Temporal Dynamics
시간에 따라 변하는 유저, 아이템의 특성을 반영하고 싶다.
아이템이 시간이 지남에 따라 인기도가 떨어진다.
유저가 시간이 흐르면서 평점을 내리는 기준이 엄격해진다.
시간을 반영한 평점 예측
학습 파라미터가 시간을 반영하도록 모델 설계
$$ \tt \widehat r_{ui}(t) = \mu + b_u(t) + b_i(t) + p^T_uq_i(t) $$
단점
- p, q 변수가 2개라서 빠른계산이 불가능하다.
- SGD를 학습하는 과정에서 업데이트를 여러 번 하기 때문에 빠른 계산이 불가능하다는 단점이 누적된다.
- 유저 수와 아이템 수가 커질수록 반복문으로 인한 연산량 증가
여기서는 정답 횟수를 행렬의 값으로 사용하였지만 문제별로 사용한 시간의 평균 혹은 다른 feature를 값으로 활용한다면 다른 잠재 요인 값들을 얻어낼 수 있다.
$R \approx PQ^{T}$
$R$: 유저들에 대한 문제별 정답 횟수 행렬$P$: 유저와 잠재 요인의 행렬$Q$: 문제와 잠재 요인의 행렬
참고하면 좋은 자료