간단 요약
확률 분포의 불확실성을 의미한다.
정보 이론에서의 엔트로피는 (최적화된 전략 하에서의) 질문 개수에 대한 기댓값이다.
스무 고개로 정답 맞추기를 진행할 때 질문이 많이 필요할수록 불확실성이 높은 것이다.
확률 분포의 무작위성(불확실성)을 측정하는 함수
$$
H(X)=\sum_{i=1}^n p_i\left(\log \frac{1}{p_i}\right)=-\sum_{i=1}^n p_i \log p_i
$$
-
entropy 공식은 왜 이렇게 생겼을까?
스무 고개로 정답 맞추기를 진행할 때 확률 분포가 불확실할수록 필요한 질문의 개수가 늘어난다.
이 때, 전체 경우를 양분하는 질문의 개수는
$log_2$를 통해 파악할 수 있다.즉, 위의 수식은 각 경우
$(p_i)$에 도달하기까지 전체 경우의 수를 이분하는 질문$(-\log_2(p_i))$이 얼마나 많이 필요한 지와 동일하게 생각할 수 있다.
ex) 1이 나올 확률이 매우 높은 찌그러진 주사위인 경우
언제나 최선의 전략을 짤 수 있는 사람이 주사위 숫자 맞추기 게임을 한다고 가정하자.
스무 고개를 진행하면 1인가?를 먼저 물어보고, 대부분 정답이 될 것이다.
하지만 공정한 주사위의 숫자를 한 번의 질문으로 예측하기는 어렵다.
따라서, 공정한 주사위의 불확실성이 찌그러진 주사위의 불확실성보다 높다.
즉, 공정한 주사위의 Entropy가 찌그러진 주사위의 Entropy보다 높다.
-
엔트로피 계산 예제
$$ X = \{ a=\frac{1}{2},b=\frac{1}{4},c=\frac{1}{8},d=\frac{1}{8}\} $$$$ \begin{matrix} H(X) &=& -(\frac{1}{2}\log\frac{1}{2} + \frac{1}{4}\log{\frac{1}{4}} + \frac{1}{8}\log{\frac{1}{8}} + \frac{1}{8}\log{\frac{1}{8}})\\\\ &=& (\frac{1}{2} + \frac{1}{2} + \frac{3}{4})\log 2\\\\ &=& 0.52680249241 \end{matrix} $$-
동전의 엔트로피
$$ H_{\text {coin }}(x)=-\left(\frac{1}{2} \log \frac{1}{2}+\frac{1}{2} \log \frac{1}{2}\right)=0.3010 $$ -
주사위의 엔트로피
$$ H_{\text {dice }}(x)=-\left(\frac{1}{6} \log \frac{1}{6}+ \cdots+ \frac{1}{6} \log \frac{1}{6}\right)=0.7782 $$
-
엔트로피의 특성
$H(X)$는 오목하다.$H\left(p_{\max }, 1-p_{\max }\right) \leq H(P)$.$H\left(p_1 q_1, \ldots, p_1 q_m, p_2 q_1, \ldots, p_2 q_m, \ldots p_n q_1, \ldots, p_n q_m\right)\\= H\left(p_1, \ldots, p_n\right)+\mathcal{S}\left(q_1, \ldots, q_m\right)$
(Shannon) Entropy
-
X를 확률 질량 함수가 P(.)인 랜덤 이산 변수라고 할 때,
X의 Entropy
$H(X)$는 다음과 같이 정의할 수 있다.$$ H(X) = -\sum_xP(x)\log_bP(x) $$
엔트로피는 자신의 정보(최적화된 전략 하에서의 질문 개수)에 대한 기댓값으로 해석될 수 있다.
$$
H(X) = -E[\log_bP(X)]
$$
b = 2의 경우, 엔트로피의 단위를 bit라고 한다.
→ X에 포함된 모든 정보를 인코딩하는 데 필요한 최소 값을 bit 단위로 추정할 수 있다.
연속형 변수의 엔트로피는 합을 적분으로 대체함으로써 정의할 수 있다.
Joint Entropy
$$
H(X, Y)=-\sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} p(x, y) \log p(x, y)
$$
ex)
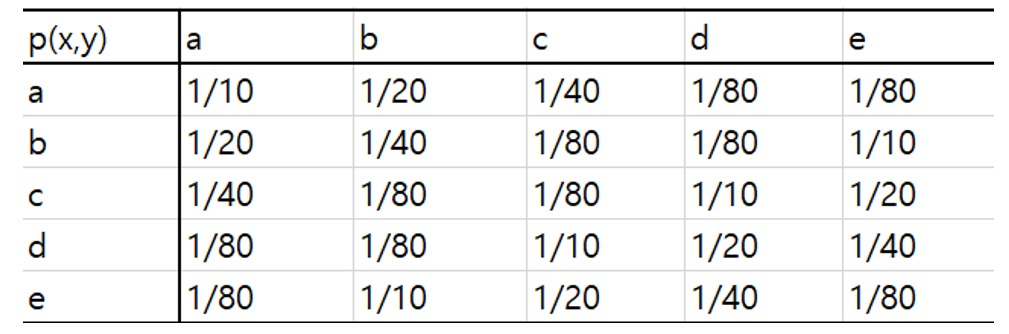
$$
\begin{aligned}H(X, Y) & =-\sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} p(x, y) \log p(x, y) \\& =-5\left[\frac{1}{10} \log \frac{1}{10}+\frac{1}{20} \log \frac{1}{20}+\frac{1}{40} \log \frac{1}{40}+\frac{1}{80} \log \frac{1}{80}+\frac{1}{80} \log \frac{1}{80}\right] \\& =\log 5\left[\frac{1}{2} \log \frac{1}{2}+\frac{1}{4} \log \frac{1}{4}+\frac{1}{8} \log \frac{1}{8}+\frac{1}{16} \log \frac{1}{16}+\frac{1}{16} \log \frac{1}{16}\right] \\& =\frac{15}{8} \log 5\end{aligned}
$$
Theorem — Independent Random Variable X,Y
$$
\mathrm{H}(\mathbf{X, Y})=\mathrm{H}(\mathbf{X})+\mathrm{H}(\mathbf{Y})
$$
증명
$$
\begin{aligned}p\left(x_i, y_j\right) & =p\left(x_i\right) p\left(y_j\right) \\H(X, Y) & =-\sum_{i=1}^N \sum_{j=1}^M p\left(x_i, y_j\right) \log \left\{p\left(x_i, y_j\right)\right\} \\& =-\sum_{i=1}^N \sum_{j=1}^M p\left(x_i\right) p\left(y_j\right) \log \left\{p\left(x_i\right) p\left(y_j\right)\right\} \\& =-\sum_{i=1}^N \sum_{j=1}^M p\left(x_i\right) p\left(y_j\right)\left[\log \left\{p\left(x_i\right)\right\}+\log \left\{p\left(y_i\right)\right\}\right] \\& =-\sum_{i=1}^N \sum_{j=1}^M p\left(x_i\right) p\left(y_j\right) \log \left\{p\left(x_i\right)\right\}-\sum_{i=1}^N \sum_{j=1}^M p\left(x_i\right) p\left(y_j\right) \log \left\{p\left(y_i\right)\right\} \\& =-\sum_{i=1}^N p\left(x_i\right) \log \left\{p\left(x_i\right)\right\}-\sum_{j=1}^M p\left(y_j\right) \log \left\{p\left(y_i\right)\right\} \\& =H(X)+H(Y)\end{aligned}
$$
Cross-Entropy(=Log loss, 교차 엔트로피)
Von Neumann Entropy(폰 노이만 엔트로피)
The von Neumann entropy of a density matrix $\boldsymbol{\rho}$, denoted by $\mathbf{H}(\boldsymbol{\rho})$, is defined as
$$
\mathbf{H}(\rho)=-\operatorname{tr}(\rho \ln \rho)=-\sum_{i=1}^n \lambda_i \ln \lambda_i
$$
where $\lambda_1, \ldots, \lambda_n$ are eigen values of $\rho$. It is conventional to define $0 \ln 0=0$.
This definition is a proper extension of both the Gibbs entropy and the Shannon entropy to the quantum case.
Relative Entropy(상대 엔트로피)
Kullback-Leibler Divergence