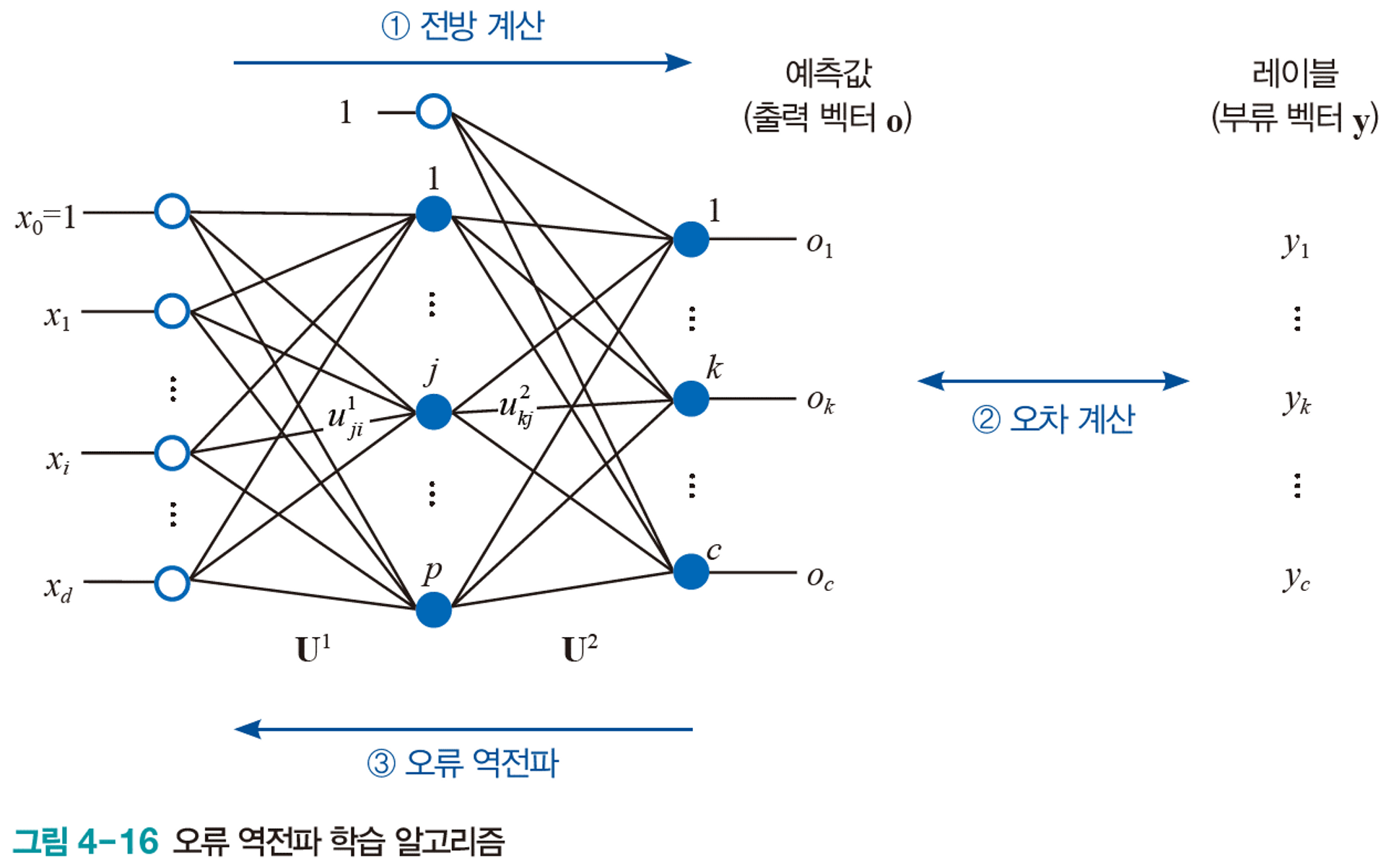
이 알고리즘으로 인해 ML Network에서의 학습이 가능하다는 것이 알려져, 암흑기에 있던 신경망 학계가 다시 관심을 받게 되었다.
출력층에서 시작하여 역방향으로 오류를 전파한다는 뜻에서 오류 역전파라 부른다.
- 내가 뽑고자 하는 target값과 실제 모델이 계산한 출력의 차이를 계산한다.
- 오차값을 다시 뒤로 전파해가면서 각 노드가 가지고 있는 변수들을 갱신한다.
직관적인 이해는 끝났다. 이제 제대로 이해해보자.
오차 역전파가 중요한 이유를 알고 싶다면, 여기를 클릭하여 오차 역전파가 없을 시에 발생하는 문제점을 이해하자.
오차 역전파
신경망을 학습하는 방법.
연쇄 법칙을 활용하여 수치 미분에서의 연산량을 대폭 감소시킨다.
수치 미분과 마찬가지로 손실 함수 위에서의 가중치의 기울기를 알게 해준다.
즉, 해당 가중치가 얼마나 오차에 영향을 끼치는지 알게 해준다.
(기울기에 대한 손실 함수의 미분)
특정 가중치 w에 대해, 오차 L 위에서의 기울기는 $\partial L\over \partial w$이다.
연쇄 법칙(chain rule)
합성 함수의 미분은 합성 함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다.
$$
{\partial z\over \partial x} = {\partial z\over \partial t}{\partial t\over \partial x}
$$
합성 함수
여러 함수로 구성된 함수
- ex)
$z = (x + y)^2$$z = t^2$$t = x + y$
순전파, 역전파, 국소적 계산
ex) $f(x) = y$
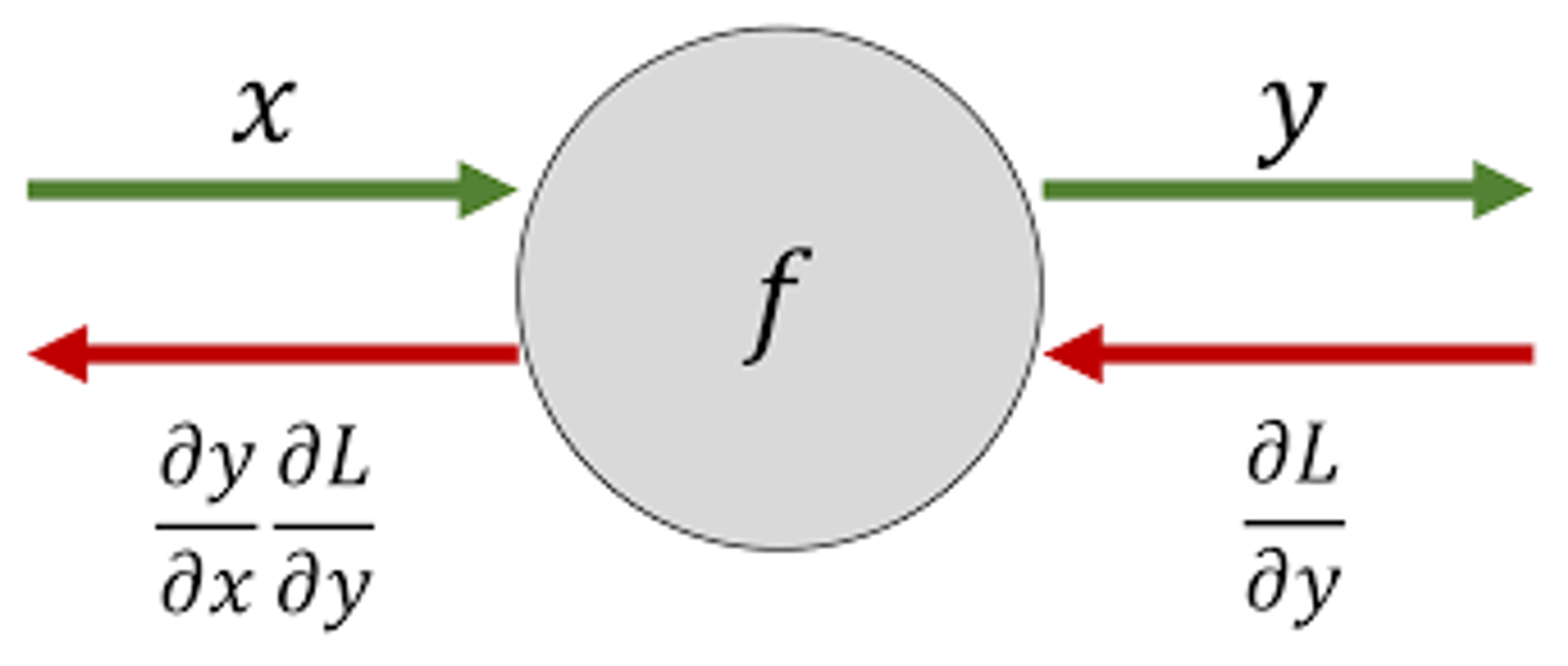
f에 x를 집어넣으면 y가 튀어나온다.
위의 그림처럼 어딘가에서 갑자기 등장한 $L$이라는 함수를 $y$로 미분한 값($\partial L\over \partial y$)이 제공된다면?
우리는 $L$이라는 함수를 모르지만, $x$로 미분한 값을 알 수 있다.
연쇄법칙을 활용하면 된다.
$$
{\partial L\over \partial x} = {\partial L\over \partial y}{\partial y\over \partial x}
$$
우리는 $\partial L\over \partial y$를 알고 있으니, $\partial y\over \partial x$만 계산하면 된다.
${\partial y\over \partial x} = f'(x)$이므로, x에 대한 함수인 $f(x)$를 미분하면 된다.
ex) $f(x) = x^2 ⇒ f'(x) = 2x$
이 때, 위의 예시에서 왼쪽에서 오른쪽으로 진행하는 단계를 순전파(forward propagation),
오른쪽에서 왼쪽으로 진행하는 단계를 **역전파(backward propagation)**이라고 한다.
국소적 계산
전체에서 어떤 일이 벌어지든 상관없이 자신과 관계된 정보만을 결과로 출력할 수 있다.
위의 예시처럼, 각 단계에서는 그저 $f(x)$의 미분값만 곱해서 하류로 흘러보낸 것이 전부다.
단순한 국소적 계산이 연결되어 전체를 구성하는 복잡한 계산을 수행하게 된다.
덧셈 노드에서의 역전파
ex) $z = x + y$
$\partial z\over \partial x$= 1$\partial z\over \partial y$= 1
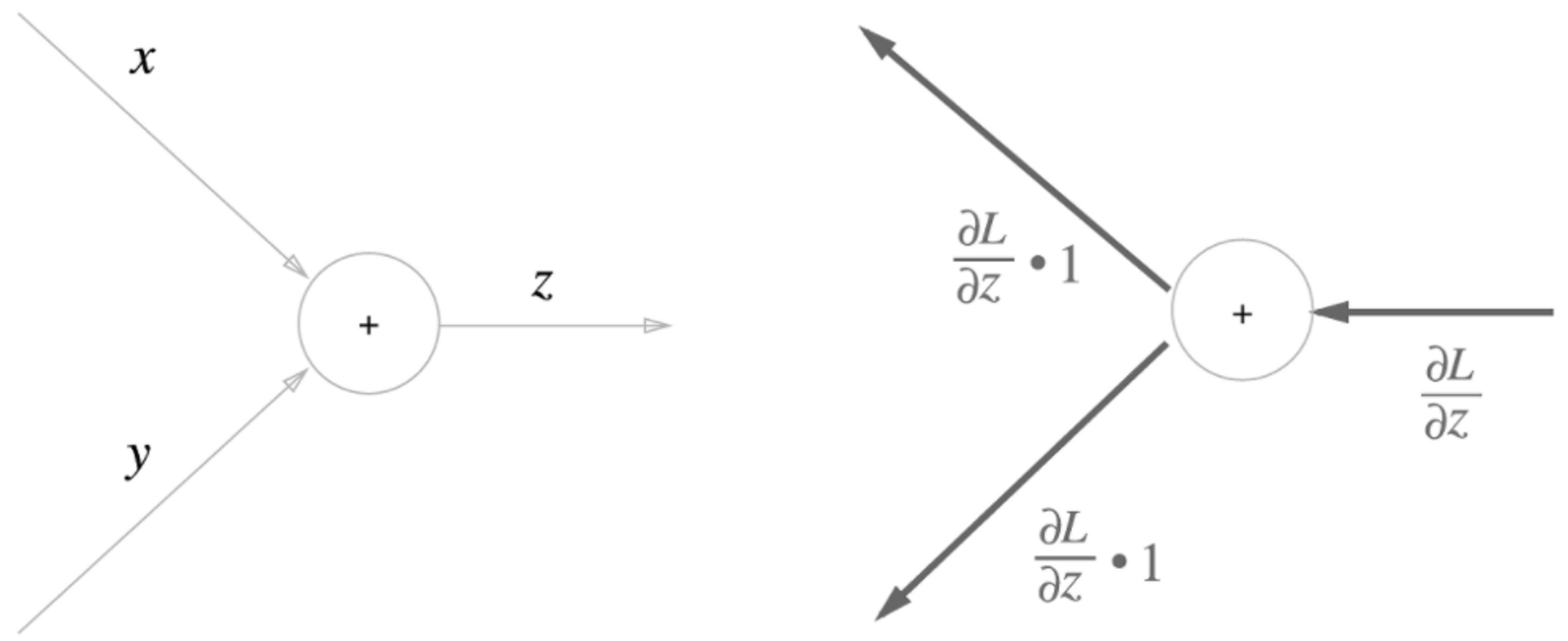
상류에서 내려온 신호인 $\partial L\over \partial z$에 $\partial z\over \partial x$를 곱함으로써 $\partial L\over \partial x$을 구했다.
단순한 덧셈 연산이기 때문에 미분값은 1이다.
즉, 덧셈에서는 상류에서 내려온 값을 그대로 하류로 전달한다.
곱셈 노드에서의 역전파
ex) $z = xy$
${\partial z\over \partial x} = y$${\partial z\over \partial y} = x$
이므로,
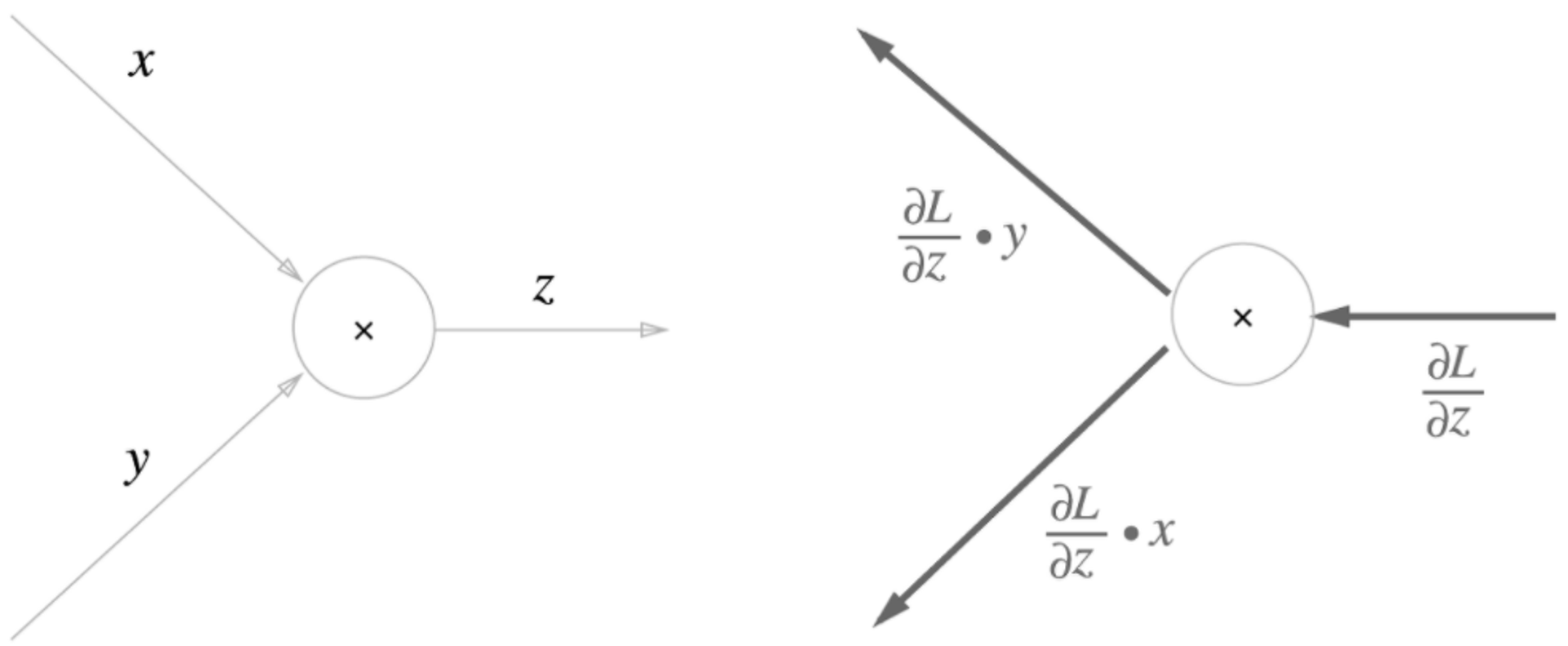 이 된다.
이 된다.
즉, 단순한 곱셈 노드는 상류에서 내려온 신호를 교차시켜 곱한 후, 다시 하류로 보낸다.
하지만 본질은 미분이다.
$z = x^2$의 경우, 미분값은 $2x$가 되는 것을 명심하자.
연쇄 법칙과 계산 그래프
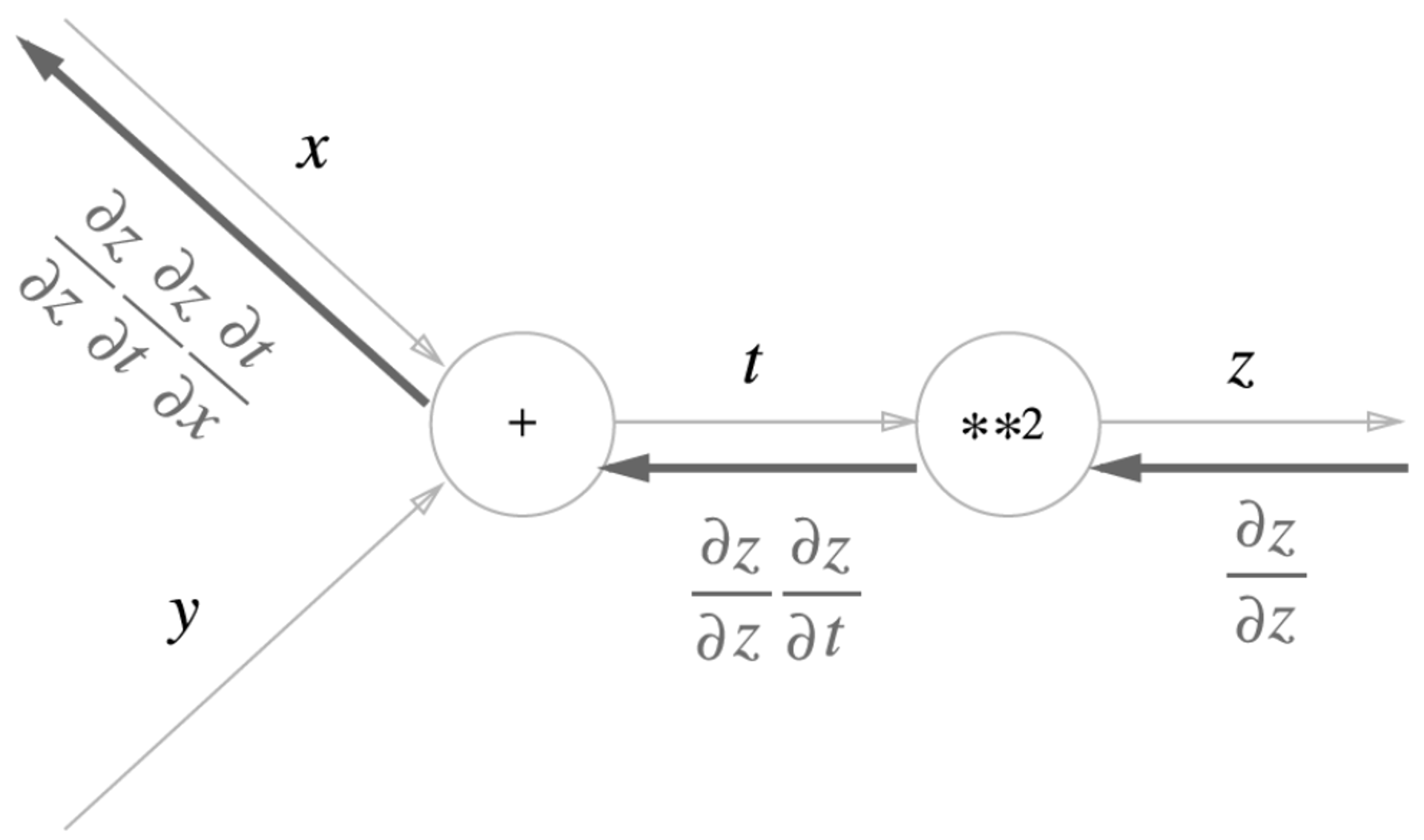
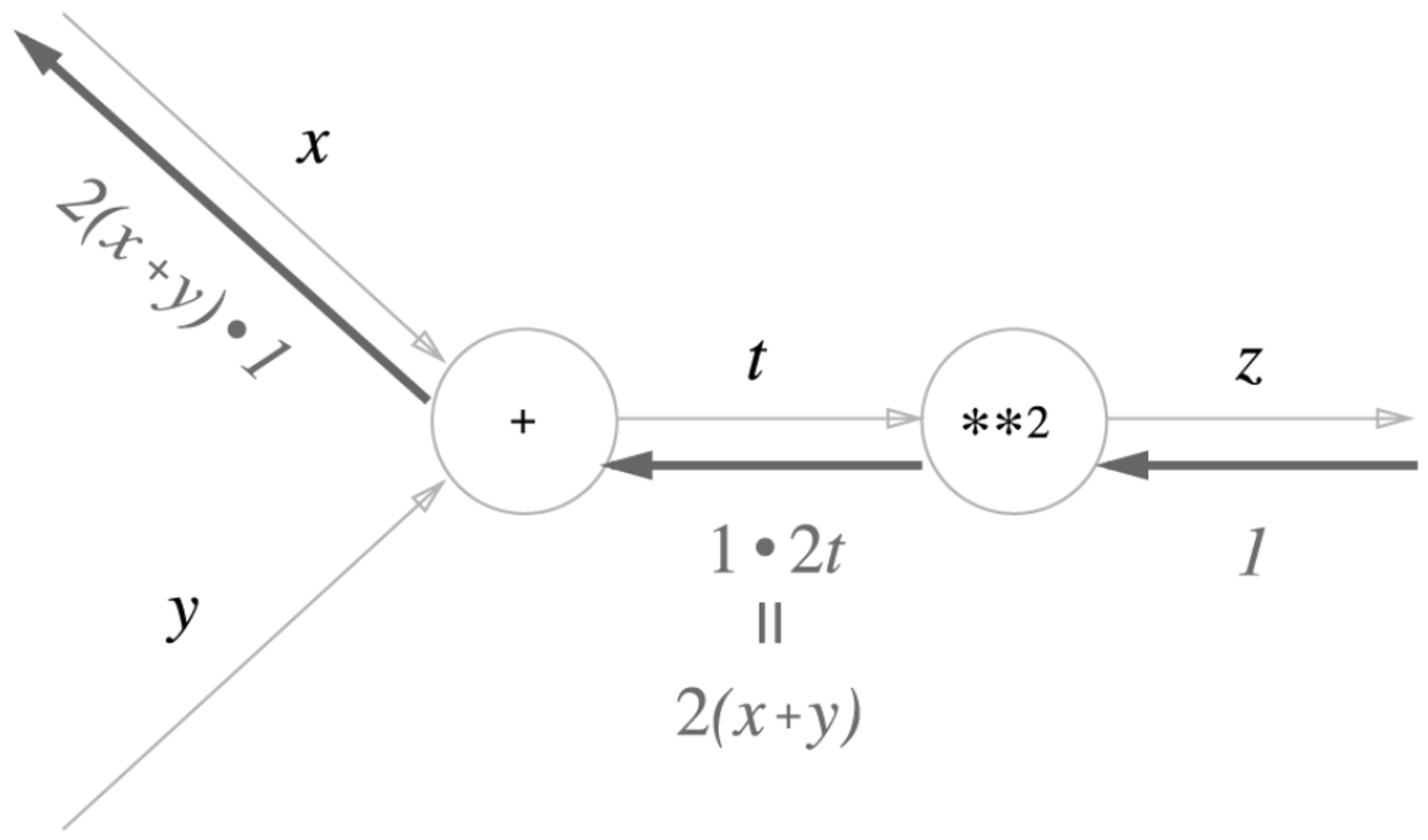
처음에 예시로 들었던 함수 $z = (x+y)^2$를 그래프화 한 것이다.
결론
역전파는 오차(손실 함수)를 상류에서 하류로 내려보내면서 각 가중치가 손실 함수에서의 기울기를 알 수 있도록 해주는 기법이다.
이 때 수많은 노드와 복잡한 활성화 함수 등이 각 노드에서 국소적 계산을 한다.
이런 값들이 누적되고 확산되어 단 한번의 신경망 계산(역방향)만으로도 모든 가중치와 편향을 갱신할 수 있다.
곱셈 노드, 덧셈 노드뿐만 아니라 exp 노드, log 노드 등 수많은 노드들이 있지만,
결국 기본 원리는 상류 노드에 해당 노드에서의 미분 값을 찾아서 곱한 뒤, 하류로 흘려보내는 것이 전부이다.
그러므로 수치 미분보다는 당연히 빠르다.
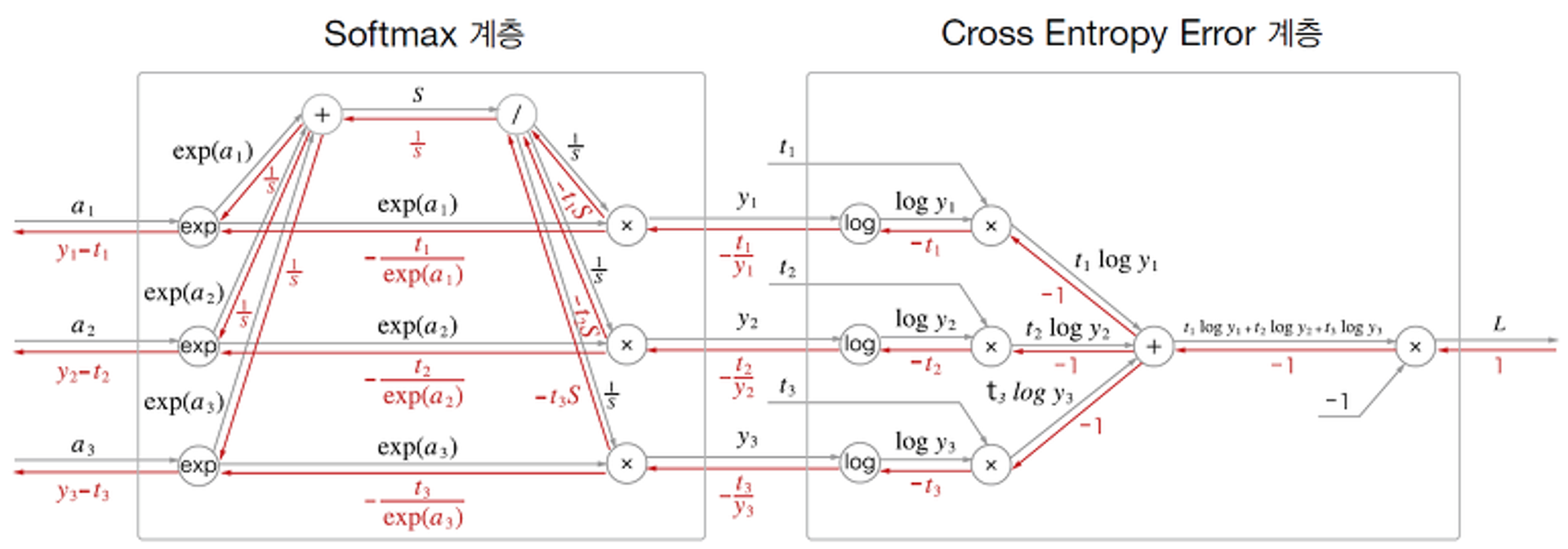
-
구현 코드
class MulLayer: # 곱셈 계층 def __init__(self) -> None: self.x = None self.y = None def forward(self, x, y): # 순전파, x와 y의 값을 저장해야만 backward때 사용할 수 있다. self.x = x self.y = y out = x * y return out def backward(self, dout): # 역전파로 상위 계층에서의 미분 값 * 반대 노드의 값을 출력한다. dx = dout * self.y dy = dout * self.x return dx, dy class AddLayer: # 덧셈 계층 def __init__(self) -> None: pass def forward(self, x, y): # 순전파, x와 y 값을 저장하지 않아도 된다. out = x + y return out def backward(self, dout): dx = dout * 1 dy = dout * 1 return dx, dy